制御工学博士の日常+備忘録

ようやく制御工学で博士を手に入れたので真っ当な人間になるべく研究以外の事とか色々と備忘録的にやっていく。そんな感じ

トップ > 研究 > 作業空間オブザーバに出てくる等価質量行列の算出法のメモ

作業空間オブザーバに出てくる等価質量行列の算出法のメモ

研究 制御工学 勉強

どうも。kwaz6です。
今回はロボットのモーションコントロールにおいて、作業空間オブザーバで作業空間上で外乱オブザーバによる加速度制御を構成する手法の紹介とその中で、等価質量行列があるのでそれがどうやって導出されるか、実際に確認したのでまとめておく。

外乱オブザーバのおさらい

外乱オブザーバ(Disturbance Observer: DOB)とは、あるプラントの入出力間を比較し、その間にある外乱を推定するものです。
このことを単慣性系の簡単なモデルで考えてみます。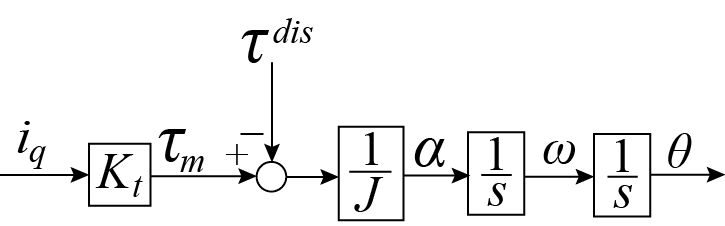

f:id:kwaz6:20200506045102p:plain:w320
図1 単慣性系のモータプラントモデル

図1において、i_q, K_t \tau_m, \tau^{dis}, J, \alpha, \omega, \thetaはモータ電流、トルク定数、モータトルク、外乱トルク、モータイナーシャ、モータ加速度、モータ速度、モータ位置を表す。
ここで、上記の外乱オブザーバの定義に基づいて考える。

入力は電流i_qで出力は\thetaなので、仮に外乱トルク\tau^{dis}が無ければ、モータは入力電流でのみ動作する。つまり、入力電流さえ分かっていれば思い通りのモータ制御ができることになる。

しかしながら、実際には外乱トルクが存在するため、電流入力に外乱トルクが加わった後のモータ位置が出力される。入力電流と外乱トルクが既知であるなら、出力位置も予測が可能だが、実際は外乱トルクは完全には検出できない場合が多くある。(例えば、摩擦、ロボットの動力学、接触力、パラメータ変動など)

通常は外乱トルク以外の情報が既知となっています。つまり出力の位置と入力電流が既知で、間にあるモータイナーシャJやトルク定数K_tも既知の時、印可された外乱トルクが逆算できることになる。この考えを利用したのが外乱オブザーバとなります。
では、具体的に計算式を示します。

電流と外乱トルクを入力としてモータ位置を出力とした時、モータ速度までの式は

\omega=\frac{1}{Js}(K_t i_q - \tau^{dis})

となります。この式から\tau^{dis}について整理すると、

\tau^{dis}=K_t i_q - Js\omega

sはラプラス領域で微分\frac{d}{dt}を意味しますが、実際のシステムでは全周波数領域で微分することは不可能ですし、ノイズ信号も微分するため、制御の際には都合が悪くなります。そこで、全体にローパスフィルタを掛けて外乱トルクを推定します。

\hat{\tau}^{dis}=\frac{g_d}{s+g_d}(K_t i_q - Js\omega)

また、実際のプラントパラメータと設計上のプラントパラメータを区別するために、パラメータは添え字に_nを付け、ノミナル値と実際の値で区別することが一般的です。また、上式の実装において、実際に微分は使いたくないので、数学テクニックを用いて最終的には次のような形になります。

\hat{\tau}^{dis}=\frac{g_d}{s+g_d}(K_{tn} i_q + J_ng_d\omega) - J_ng_d\omega

これが、一般に知られている外乱オブザーバの式となります。
ということで実際のブロック図を示すと次のような形になります。

f:id:kwaz6:20200506054357p:plain:w320
図2 外乱オブザーバ

ちなみにもう少し深く学ぶとモータプラントのモータ速度、外乱トルク(ステップ関数と定義)の2状態に対して状態方程式を立て、そこからゴピナス法によって最小次元オブザーバの構成にすると、図2に示すような外乱オブザーバになります。ただ、最小次元オブザーバは慣れないと解くのが面倒なので、外乱オブザーバを構成したければ、ざっくり「プラントモデルの逆数と入力信号の差分にフィルタを掛けたら外乱オブザーバになる」と思っておけば良いと思います。
(\hat{\tau}^{dis}=\frac{g_d}{s+g_d}(K_t i_q - Js\omega))

さて、ここまでで外乱オブザーバをおさらいしたので、次に、作業空間オブザーバに入っていきたいと思います。

作業空間オブザーバ

外乱オブザーバと同様で作業空間オブザーバも同じ構成をすることができます。
違いと言えば、外乱オブザーバはモータ一つ、つまりロボットの1軸分しかやってなかったのに対して、作業空間オブザーバはロボット全体を一つのプラントシステムとして捉えて外乱オブザーバを構成するところです。
実際の図を示します。

f:id:kwaz6:20200506055756p:plain:w320
図3 作業空間オブザーバ

図3に示すように作業空間上でも外乱オブザーバと同様の構成が可能です。しかし、ここで注意なのが質量行列Mです。これは3軸ロボットを例にしますが、実際には質量行列が質量の対角行列diag(M)となることはなく、ロボットの姿勢によってはすべての行列要素に値を持ちます。したがって、作業空間オブザーバを構成するときには等価質量行列を求めてそれをノミナル値とします。

等価質量行列の導出

今回参考にした論文はこちらです。

村上、大西：「ロバスト制御に基づいた多自由度ロボットの安定性および作業空間での非干渉制御に関する一考察」, 電学論D, Vol. 113, No. 5, pp. 639-646 (1993)

上記の資料を参考にすると、導出にはロボットの関節空間と作業空間双方において外乱が無視できると仮定しております。その上で関節空間、作業空間双方の運動エネルギーが等価であるという仮定から導出しています。

まず、関節空間、作業空間の運動エネルギーは

K_{joint}=\{\frac{1}{2}\dot{q}^TJ_n\dot{q}\}\\ K_{work}=\{\frac{1}{2}\dot{x}^TM_n\dot{x}\}
となる。ここで、qはロボットの関節位置です。一番上の外乱オブザーバでは\thetaで表記してます。
ここで、作業空間と関節空間の速度の関係をヤコビアンJ_{aco}を用いて表すと、
\dot{q}=J_{aco}^{-1}\dot{x}
となり、これにより
K_{joint} = \{\frac{1}{2}\dot{q}^TJ_n\dot{q}\} = \{\frac{1}{2} (J_{aco}^{-1}\dot{x} )^T J_n (J_{aco}^{-1}\dot{x} )\} \\

ここで、転置行列の性質((A B)^T=B^T A^T)を利用する。すると

K_{joint} = \{\frac{1}{2} (J_{aco}^{-1}\dot{x} )^T J_n (J_{aco}^{-1}\dot{x} )\} = \{\frac{1}{2} \dot{x}^T (J_{aco}^{-1})^T J_n J_{aco}^{-1} \dot{x} \}

従って、K_{work}と比較すると、等価質量行列M_nは

M_{n} = (J_{aco}^{-1})^T J_n J_{aco}^{-1} = J_{aco}^{-T} J_n J_{aco}^{-1}

と求められる。
ちなみに等価質量行列を対角行列として設定すれば、作業空間上の各軸方向非干渉化が可能であるが、どうも作業空間オブザーバ関連の論文を他にも読むと対角行列要素をノミナル値に設定するよりも、等価質量行列の値そのものをノミナルに設定した方が制御系が安定になるらしい。この辺りは追々勉強したいと思う。

まとめ

今回は作業空間オブザーバに用いられる等価質量行列の算出過程を備忘録的にまとめた。

作業空間上の等価質量行列は以下より求められる。

M_{n} = (J_{aco}^{-1})^T J_n J_{aco}^{-1} = J_{aco}^{-T} J_n J_{aco}^{-1}
よくわからなくてもこの式を利用するだけで、実装できるので今後シミュレーション等で確認していきたい。

また、より詳しい外乱オブザーバの記事についてはこちらの方がよくまとまっているので参考になると思います。
外乱オブザーバの紹介 - Qiita

それでは。